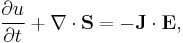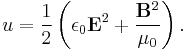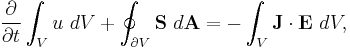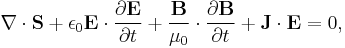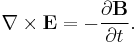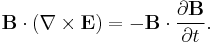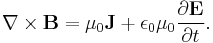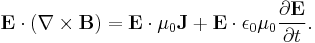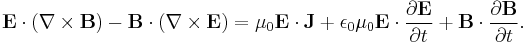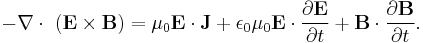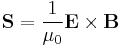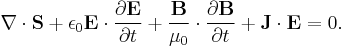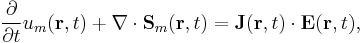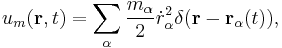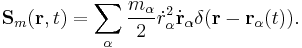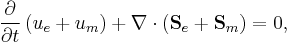Poynting's theorem

Poynting's theorem is a statement due to British physicist John Henry Poynting[1] about the conservation of energy for the electromagnetic field. Poynting's theorem takes into account the case when the electric and magnetic fields are coupled – static or stationary electric and magnetic fields are not coupled. In other words, Poynting theorem is valid only in electrodynamics. It relates the time derivative of the energy density, u to the energy flow and the rate at which the fields do work. It is summarised by the following formula:

\frac{\partial u}{\partial t} %2B \nabla\cdot\mathbf{S} = -\mathbf{J}\cdot\mathbf{E},

where S is the Poynting vector representing the flow of energy, J is the current density, E is the electric field and u is the energy density defined by (symbol ε0 is the electric constant and μ0 is the magnetic constant):

u = \frac{1}{2}\left(\epsilon_0 \mathbf{E}^2 %2B \frac{\mathbf{B}^2}{\mu_0}\right).

Since the magnetic field does no work, the right hand side gives the negative of the total work done by the electromagnetic field per second·meter3.

Poynting's theorem in integral form:

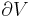\frac{\partial}{\partial t} \int_V u \ dV %2B \oint_{\partial V}\mathbf{S} \ d\mathbf{A} = -\int_V\mathbf{J}\cdot\mathbf{E} \ dV,

where \partial V \! is the surface which bounds (encloses) volume V \!.

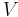In electrical engineering context the theorem is usually written with the energy density term u expanded in the following way, which resembles the continuity equation:

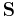\nabla\cdot\mathbf{S} %2B \epsilon_0 \mathbf{E}\cdot\frac{\partial \mathbf{E}}{\partial t} %2B \frac{\mathbf{B}}{\mu_0}\cdot\frac{\partial\mathbf{B}}{\partial t} %2B \mathbf{J}\cdot\mathbf{E} = 0,

where \mathbf{S} is the energy flow of the electromagnetic wave, 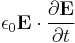\epsilon_0 \mathbf{E}\cdot\frac{\partial \mathbf{E}}{\partial t} is the density of reactive power driving the build-up of electric field, 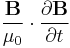\frac{\mathbf{B}}{\mu_0}\cdot\frac{\partial\mathbf{B}}{\partial t} is the density of reactive power driving the build-up of magnetic field, and 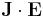\mathbf{J}\cdot\mathbf{E} is the density of real power dissipated by the Lorentz force acting on charge carriers.

Contents

Derivation

The theorem can be derived from two of Maxwell's Equations. First consider Faraday's Law:

\nabla \times \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t}.

Taking the dot product of this equation with 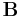\mathbf{B} yields:

\mathbf{B} \cdot (\nabla \times \mathbf{E}) = - \mathbf{B} \cdot \frac{\partial \mathbf{B}}{\partial t}.

Next consider the Ampère-Maxwell law equation:

\nabla \times \mathbf{B} = \mu_0 \mathbf{J} %2B \epsilon_0 \mu_0 \frac{\partial \mathbf{E}}{\partial t}.

Taking the dot product of this equation with 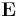\mathbf{E} yields:

\mathbf{E} \cdot (\nabla \times \mathbf{B}) = \mathbf{E} \cdot \mu_0 \mathbf{J} %2B \mathbf{E} \cdot \epsilon_0 \mu_0 \frac{\partial \mathbf{E}}{\partial t}.

Subtracting the first dot product from the second yields:

\mathbf{E} \cdot (\nabla \times \mathbf{B}) - \mathbf{B} \cdot (\nabla \times \mathbf{E}) = \mu_0 \mathbf{E} \cdot \mathbf{J} %2B \epsilon_0 \mu_0 \mathbf{E} \cdot \frac{\partial \mathbf{E}}{\partial t} %2B \mathbf{B} \cdot \frac{\partial \mathbf{B}}{\partial t}.

Finally, by the product rule, as applied to the divergence operator over the cross product (described here):

- \nabla\cdot\ ( \mathbf{E} \times \mathbf{B} ) = \mu_0 \mathbf{E} \cdot \mathbf{J} %2B \epsilon_0 \mu_0 \mathbf{E} \cdot \frac{\partial \mathbf{E}}{\partial t} %2B \mathbf{B} \cdot \frac{\partial \mathbf{B}}{\partial t}.

Since the Poynting vector 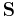\mathbf{S} is defined as:

\mathbf{S} = \frac{1}{\mu_0} \mathbf{E} \times \mathbf{B}

this is equivalent to:

\nabla\cdot\mathbf{S} %2B \epsilon_0 \mathbf{E}\cdot\frac{\partial \mathbf{E}}{\partial t} %2B \frac{\mathbf{B}}{\mu_0}\cdot\frac{\partial\mathbf{B}}{\partial t} %2B \mathbf{J}\cdot\mathbf{E} = 0.

Generalization

The mechanical energy counterpart of the above theorem for the electromagnetical energy continuity equation is

\frac{\partial}{\partial t} u_m(\mathbf{r},t) %2B \nabla\cdot \mathbf{S}_m (\mathbf{r},t) = \mathbf{J}(\mathbf{r},t)\cdot\mathbf{E}(\mathbf{r},t),

where u_m is the mechanical (kinetic) energy density in the system. It can be described as the sum of kinetic energies of particles α (e.g., electrons in a wire), whose trajectory is given by 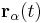\mathbf{r}_{\alpha}(t):

u_m(\mathbf{r},t) = \sum_{\alpha} \frac{m_{\alpha}}{2} \dot{r}^2_{\alpha} \delta(\mathbf{r}-\mathbf{r}_{\alpha}(t)),

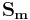\mathbf{S_m} is the flux of their energies, or a "mechanical Poynting vector":

\mathbf{S}_m (\mathbf{r},t) = \sum_{\alpha} \frac{m_{\alpha}}{2} \dot{r}^2_{\alpha}\dot{\mathbf{r}}_{\alpha} \delta(\mathbf{r}-\mathbf{r}_{\alpha}(t)).

Both can be combined via the Lorentz force, which the electromagnetical fields exert on the moving charged particles (see above), to the following energy continuity equation or energy conservation law:[2]

\frac{\partial}{\partial t}\left(u_e %2B u_m\right) %2B \nabla\cdot \left( \mathbf{S}_e %2B \mathbf{S}_m\right) = 0,

covering both types of energy and the conversion of one into the other.

Alternative forms

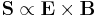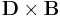It is even possible to derive alternative versions of Poynting's theorem.[3] Rather than using the flux vector \mathbf{S} \propto \mathbf{E} \times \mathbf{B} as above, it is possible to follow the same style of derivation, but instead choose the Abraham form \mathbf{E} \times \mathbf{H}, the Minkowski form \mathbf{D} \times \mathbf{B}, or even the novel form 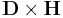\textbf{D} \times \textbf{H}. Each choice represents the response of the propagation medium in its own way: the 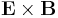\mathbf{E} \times \mathbf{B} form above has the elegant property of doing this with only electric currents, whilst the 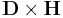\textbf{D} \times \textbf{H} form uses only (fictitious) magnetic monopole currents. The other two forms (Abraham and Minkowski) use complementary combinations of electric and magnetic currents to represent the polarization and magnetization responses of the medium.

Notes

  1. ^ Poynting, J. H. (1884). "On the Transfer of Energy in the Electromagnetic Field". Philosophical Transactions of the Royal Society of London 175: 343–361. doi:10.1098/rstl.1884.0016. 
  2. ^ Richter, E.; Florian, M.; Henneberger, K. (2008). "Poynting's theorem and energy conservation in the propagation of light in bounded media". Europhysics Letters 81 (6): 67005. arXiv:0710.0515. Bibcode 2008EL.....8167005R. doi:10.1209/0295-5075/81/67005. 
  3. ^ Kinsler, P.; Favaro, A.; McCall M.W. (2009). "Four Poynting theorems". European Journal of Physics 30 (5): 983. arXiv:0908.1721. Bibcode 2009EJPh...30..983K. doi:10.1088/0143-0807/30/5/007. 

External links